Топографическая карта

Содержание:

Справка
Проблема с потоком
Индивидуальные доказательства
Карты переходов
Предназначение топосъёмки
Рекомендации
Рельеф
Формальное определение
Сущность и виды топосъёмки
Географические карты
Правила для точек
Определения и термины
Дизайн карты
Расстояния и масштабы
- Как определить расстояние?
- Использование карт с различными масштабами
Больше структуры
Цели
Ориентация карт
Методы
- Полевое исследование

Справка

Топология карты создает топологические отношения между общими частями объектов. что позволяет редактировать объекты с общей геометрией одновременно. Топологию карты можно создать для точечных, линейных или полигональных слоев из шейп-файлов или классов объектов базы геоданных. Объекты могут находится в одном или нескольких слоях различных типов.

Создать топологию карты очень легко. Необходимо только выбрать слои, участвующие в топологии, и задать кластерный допуск. Кроме того, если вы щелкните инструмент Редактировать топологию (Topology Edit), не имея действующей топологии, вам будет предложено создать ее.

Поскольку топология карты основана на слоях карты, видимость слоя, в т.ч. определяющие запросы и диапазоны масштабов, также учитывается. При использовании инструментов топологии с топологией карты, редактируются только видимые объекты. Например, у вас имеется полигональный слой, который содержит коды землепользования и административные границы, но вам нужно отредактировать только коды землепользования. Можно задать определяющий запрос к слою, чтобы отобразить только объекты с кодами землепользования и скрыть административные границы. Поскольку объекты административных границ не отображаются на карте, они не будут затронуты при редактировании топологии.

С другой стороны, в случаях, когда объекты необходимо редактировать вместе, будьте внимательны при задании определяющих запросов и отключении слоев. Например, имеется слой типов лесов с определяющим запросом, с помощью которого отображаются только лиственные породы деревьев. Вечнозеленые породы на карте не отображаются. При редактировании, обновляются только видимые лиственные породы деревьев, поэтому лес перестанет быть сплошным, т.к. на границах между лиственными и вечнозелеными породами появятся пробелы. Следует убедиться, что все объекты, которые необходимо редактировать совместно, являются видимыми, что позволит добиться топологического совпадения.

Щелкните Выделить топологию (Select Topology).

на панели инструментов Topology (Топология). Появляется диалоговое окно Выбор топологии (Select Topology).
Отметьте слои, которые будут участвовать в топологии карты. Все слои, которые сейчас находятся в текущей редактируемой области и могут участвовать в топологии, будут перечислены в диалоговом окне. Слои классов объектов аннотаций и объектов-размеров, а также классы объектов, участвующие в геометрических сетях, не могут быть включены в топологию карты, и поэтому не указываются в списке.
Дополнительно, щелкните Опции (Options), чтобы просмотреть параметры кластерного допуска, который определяет, насколько близко должны располагаться ребра или вершины, чтобы они считались смежными. Как правило, кластерный допуск, использующийся по умолчанию, менять не следует, поскольку это минимально возможное значение. Повышение кластерного допуска может уменьшить число несмежных границ или несовпадающих вершин, однако установка слишком больших значений кластерного допуска может стать причиной нарушения геометрии объектов и появления искажений.
Щелкните ОК.

Проблема с потоком

Проблема потока заключается в том, как решить следующую задачу:

Если это возможно, наименьшее натуральное число должно быть определено для данного натурального числа , для которых выбраны произвольно различные точки на замкнутой, ориентируемой поверхности пола может всегда быть соединены попарно простыми кривыми Жордана таким образом , что все эти кривые Джордан никогда не пересекают друг друга и встречаются максимум в выбранных точках .м≥3{\ displaystyle m \ geq 3}γ(м){\ Displaystyle \ gamma (м)}ЧАСγ(м){\ Displaystyle H _ {\ gamma (м)}}γ(м){\ Displaystyle \ gamma (м)}п1,п2,…,пм∈ЧАСγ(м){\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {m} \ in H _ {\ gamma (m)}}п1,п2,…,пм{\ displaystyle p_ {1}, p_ {2}, \ ldots, p_ {m}}

Как оказалось, проблему с резьбой можно решить, и это приводит к формуле

γ(м)знак равно⌈(м-3)(м-4-й)12⌉(м∈N,м≥3){\ displaystyle \ gamma (m) = \ lceil {\ frac {(m-3) (m-4)} {12}} \ rceil \; (m \ in \ mathbb {N} \ ;, \; m \ geq 3)}.

Это также показывает, что справедливость этой формулы также подразумевает справедливость уравнения идентичности Хивуда .χ(ЧАСп)знак равномп(п∈N,п>){\ displaystyle {\ chi} (H_ {p}) = m_ {p} \; (p \ in \ mathbb {N} \ ;, \; p> 0)}

Индивидуальные доказательства

хроматической число следует отличать от Эйлера характеристики из , хотя та же греческая буква появляется в качестве идентификатора для обоих номеров.χ(Ф.){\ Displaystyle \ чи (F)}Ф.{\ displaystyle F}
↑ Рудольф Фрич: Четырехцветный набор. 1994, с. 25-26, 128.
KP Müller, H. Wölpert: Иллюстративная топология. 1976, с. 67.
Müller, Wölpert, op. Cit., Стр. 148-149.
— скобочная функция Гаусса .⌊⋅⌋{\ Displaystyle \ lfloor {\ cdot} \ rfloor}
Герхард Рингель: Проблема раскраски карт. в: Selecta Mathematica III 1971, стр. 30 и сл., 45-47
↑ Рингель, указ. Соч., Стр. 31
См. !
Рингель, указ. Соч., Стр. 32
— .⌈⋅⌉{\ Displaystyle \ lceil \ cdot \ rceil}
Рингель, соч., Стр. 32-33

Карты переходов

M {\ displaystyle M}
U α {\ displaystyle U _ {\ alpha}}
U β {\ displaystyle U _ {\ beta}}
φ α {\ displaystyle \ varphi _ {\ alpha}}
φ β {\ displaystyle \ varphi _ {\ beta}}
τ α , β {\ Displaystyle \ тау _ {\ альфа, \ бета}}
τ β , α {\ displaystyle \ tau _ {\ beta, \ alpha}}
р п {\ displaystyle \ mathbf {R} ^ {n}}
р п {\ displaystyle \ mathbf {R} ^ {n}}

Две диаграммы на многообразии и соответствующие им карты переходов

Карта переходов дает возможность сравнить две диаграммы атласа. Чтобы сделать это сравнение, мы рассматриваем состав одной диаграммы с инверсией другой. Эта композиция не является четко определенной, если мы не ограничим обе карты пересечением их областей определения. (Например, если у нас есть карта Европы и карта России, то мы можем сравнить эти две карты на их пересечении, а именно европейскую часть России.)

Чтобы быть более точным, предположим , что и две карты для многообразия М такое , что является непустым . Карта перехода — это карта, определяемая
( U α , φ α ) {\ displaystyle (U _ {\ alpha}, \ varphi _ {\ alpha})} ( U β , φ β ) {\ displaystyle (U _ {\ beta}, \ varphi _ {\ beta})} U α ∩ U β {\ Displaystyle U _ {\ alpha} \ cap U _ {\ beta}} τ α , β φ α ( U α ∩ U β ) → φ β ( U α ∩ U β ) {\ displaystyle \ tau _ {\ alpha, \ beta}: \ varphi _ {\ alpha} (U _ {\ alpha} \ cap U _ {\ beta}) \ to \ varphi _ {\ beta} (U _ {\ alpha} \ cap U _ {\ beta})}

τ α , β знак равно φ β ∘ φ α — 1 . {\ displaystyle \ tau _ {\ alpha, \ beta} = \ varphi _ {\ beta} \ circ \ varphi _ {\ alpha} ^ {- 1}.}

Обратите внимание, что поскольку и являются гомеоморфизмами, отображение перехода также является гомеоморфизмом.
φ α {\ displaystyle \ varphi _ {\ alpha}} φ β {\ displaystyle \ varphi _ {\ beta}} τ α , β {\ Displaystyle \ тау _ {\ альфа, \ бета}}

Предназначение топосъёмки

Геодезическая съёмка осуществляется в таких случаях:

при разработке детальных, генеральных планов городов и других населённых пунктов, а также для составления специальных и общих инженерных топографических планов;
для обновления топографических карт и планов местности;
при проведении газовых труб, а также других трубопроводов;
во время разработки архитектурного проекта для реконструкции старых зданий и возведения новых;
при планировании размещения различных объектов (пруда, цветника, сарая, огорода, системы полива или дренажа) на придомовом участке дачного или частного жилого дома;
как основа для ландшафтного проектирования;
при освоении территорий в сельскохозяйственной сфере, для фермерских хозяйств, в водно-энергетической отрасли, для планирования инфраструктуры и плотности застройки различных осваиваемых местностей;
с целью грамотного проведения противооползневых и других подобного рода работ на местности;
для прокладки железнодорожных маршрутов, автомобильных магистралей;

Геодезический инструмент на стройкеИсточник geomergroup.ru

при проведении электрификации участка (в том числе при установке опор линий электропередач), узаконивании новых построек частных хозяйств;
для других типов работ, которые на стадии разработки требуют высокой детализации участка (например, для будущего строительства).

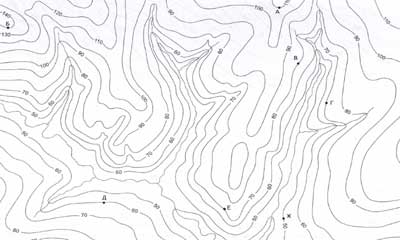
Рельеф

На топографическом плане для изображения форм рельефа используются замкнутые линии. Такие горизонтали дают объемное представление о рельефе местности.

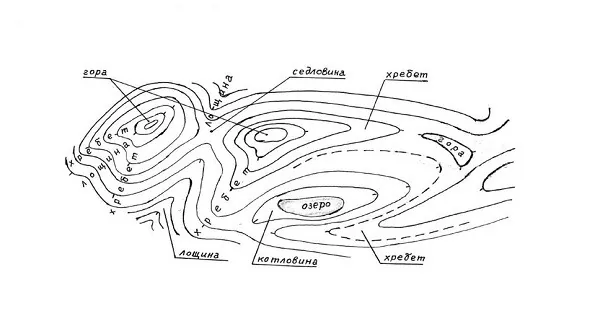
Горизонтали

Горизонталью называют линию на карте, которая соединяет точки земли с одинаковой высотой относительно уровня моря. Но те части земной поверхности, которые нельзя отобразить линиями, помечаются специальными знаками. К таким неровностям относятся овраги, обрывы, скалы.

Горизонтали рисуются на плане через одинаковые отрезки высоты. Поэтому количество горизонталей говорит читателю о высоте или глубине неровности. Чем больше и чаще расположены горизонтали, тем круче подъем или спуск. А с помощью бергштриха можно понять возвышенность на карте или яма.

Бергштрих — это черточка, проведенная перпендикулярно изолинии и указывающая свободным концом направление уменьшения величины объекта.

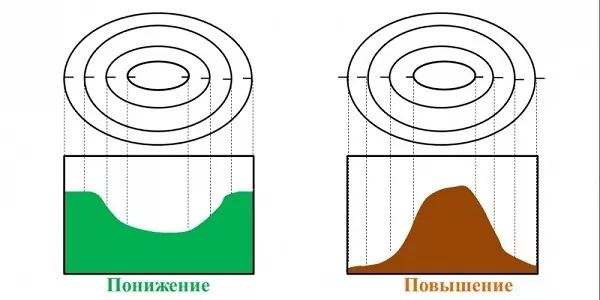
Бергштрихи

Формальное определение

Топологическое пространство X называется локально евклидовым , если существует неотрицательное целое число п такое , что каждая точка в X имеет окрестность , которая гомеоморфно к реальному п -пространство R н .

Топологическое многообразие является локально евклидова хаусдорфовым . К топологическим многообразиям обычно предъявляются дополнительные требования. В частности, многие авторы определяют их как паракомпактные или второсчетные .

В оставшейся части статьи многообразие будет означать топологическое многообразие. П-многообразие будет означать топологическое многообразие, что каждая точка имеет окрестность , гомеоморфную R н .

Сущность и виды топосъёмки

Съемка топографическая как услуга представляет собой комплекс работ, которые производятся с целью получения плана местности в виде плана, съёмочного оригинала, а также другой топографической информации. Выполняется этот процесс путём измерения углов, высот и других параметров с помощью специальных инструментов с земли, воды или воздуха. В результате топосъёмки оформляется чертёж со схематическими обозначениями различных элементов инфраструктуры. В зависимости от конечного назначения топографической съёмки на эту схему могут быть нанесены также другие объекты.

Наземная съёмка может быть комбинированной, плановой (горизонтальной), вертикальной. При этом задачей плановой топосъёмки является получение понимания взаимного расположения координат точек в горизонтальной плоскости земной поверхности.

Вертикальная геодезическая съёмка может быть нескольких видов в зависимости от технологического процесса и применяемого при этом оборудования:

стереотопографическая (такой вид топосъёмки, который использует в том числе стереопары);

Стереотопографическая съёмкаИсточник ytimg.com

гидролокационная (съёмка дна водоёмов с помощью гидролокатора, находящегося на судне);
мензульная (в данном случае применяется мензула, полевой чертёжный столик, и кипрегель, специальный геодезический прибор);
теодолитная (используется теодолит с мерами измерения лимбами, имеющими градусное и минутное деление);
тахеометрическая (при получении данных используется тахеометр, геодезический инструмент, измеряющий расстояния и углы);
аэрофотосъёмка (процесс связан с получением фотографии местности с воздуха);
буссольная (применяется буссоль или особый вид компаса, с помощью которого получают метрическую информацию о местности);
цифровая (этот вид топографической съёмки, при которой полученное изображение оцифровывается).

При осуществлении топографической съёмки крупного масштаба на получаемом плане отображаются все элементы местности: населённые пункты (границы), сады, лесные и другие насаждения, дороги автомобильные и железные, различные сооружения, инженерные и другие наземные коммуникации, а также детали рельефа.

План местности с условными обозначениямиИсточник geomergroup.ru

Географические карты

Карта звездного неба XVII века картографа Фредерика де Вит.

Картография или картографирование — это изучение и практика создания изображений Земли на плоской поверхности (см. Историю картографии ), и того, кто делает карты, называют картографом .

Дорожные карты , возможно, являются сегодня наиболее широко используемыми картами и образуют подмножество навигационных карт, которые также включают аэронавигационные и морские карты , карты железнодорожной сети, а также карты для пеших и велосипедных прогулок. В количественном отношении наибольшее количество нарисованных листов карты, вероятно, составлено местными обследованиями, проводимыми муниципалитетами , коммунальными службами, налоговыми инспекторами, поставщиками экстренных служб и другими местными агентствами. Многие национальные геодезические проекты были выполнены военными, например, British Ordnance Survey : гражданское правительственное агентство, всемирно известное своей детально проработанной работой.

В дополнение к информации о местоположении карты также могут использоваться для изображения контурных линий, указывающих постоянные значения высоты , температуры , количества осадков и т. Д.

Правила для точек

Правило топологии
Описание правила
Возможные методы исправления
Примеры
Должны совпадать с (Must Coincide With)
Требуется, чтобы точки в одном классе объектов (или подтипе) совпадали с точками в другом классе объектов (или подтипе). Это может быть полезно, когда точки должны быть покрыты другими точками, например, трансформаторы должны совпадать с питающими опорами, а точки обследования железной дороги должны совпадать со станциями.
Замкнуть (Snap): Метод перемещает точечный объект из первого класса или подтипа к ближайшей точке во втором классе или подтипе, если второй объект располагается в пределах определенного расстояния. Если поблизости не будет найдено ни одного объекта в пределах указанного допуска, точка останется незамкнутой. Метод исправления Замкнуть может быть применен к одной или нескольким ошибкам правила Должны совпадать с.

Красными квадратными маркерами показаны объекты, которые не совпадают с синими точками.

Не должны совпадать (Must Be Disjoint)
Требуется, чтобы точки располагались отдельно от других точек в пределах одного класса объектов (или подтипа). Любые точки, которые перекрываются, будут помечены как ошибки. Это может быть полезно для того, чтобы убедиться, что точечные объекты не совпадают и не дублируются в пределах одного класса или подтипу, например, города в слое с населенными пунктами, точки с номерами лотов участков и т.п.
Нет

Розовым отмечены точки, которые совпадают с синими точками, что является ошибкой.

Должны совпадать с границей
Это правило требует, чтобы точечные объекты размещались строго на границах полигональных объектов. Например, если эти точки формируют систему границ, как в случае с пограничными столбами, которые должны располагаться на ребрах полигонов.
Нет

Квадратик указывает ошибку, поскольку эта точка не лежит на границе полигона.

Должны быть полностью внутри
Это правило требует, чтобы точечные объекты располагались внутри площадных объектов. Оно применяется, когда точки связаны с полигонами, как в случае со скважинами и бассейнами добычи или адресными точками и участками.
Удалить (Delete): Метод удаляет точечные объекты, которые не находятся в пределах полигональных объектов

Обратите внимание, что вы можете использовать инструмент Редактировать (Edit), чтобы переместить точку в пределы полигона если вы не хотите удалять ее. Этот метод исправления ошибок может быть применен к одной или нескольким ошибкам правила Должны быть полностью внутри.

Квадратики указывают ошибки, где точки находятся не внутри полигона.

Должны совпадать с конечными точками
Это правило требует, чтобы точечные объекты одного класса совпадали с конечными точками линий другого класса

Это правило похоже на правило Конечные точки должны совпадать с (Endpoint Must Be Covered By), в случаях когда оно нарушается, и точечный объект становится ошибкой, а не линия.
Удалить (Delete): Метод удаляет точечные объекты, которые не совпадают с конечными точками линейных объектов. Вы можете замкнуть точку на линию, установив замыкание на ребра линейного слоя, Затем перемещая точку при помощи инструмента Редактировать. Этот способ может применяться к одной или нескольким ошибкам для правила Должны совпадать с конечными точками.

Квадратик указывает ошибку, где точка не совпадает с конечной точкой линии.

Точка должна лежать на линии
Это правило требует, чтобы точки одного класса пространственных объектов размещались на линиях другого класса пространственных объектов. Точка может также лежать на конечной точке линии. Это правило может быть полезно для точечных объектов, которые должны следовать за линейными объектами, например автодорожные значки должны располагаться вдоль автомагистрали.
Нет

Квадратиками обозначены точки, не лежащие на линии.

Определения и термины

Топологическое отображение на является , где и двумя конечными набором системы из подмножеств в а также представляет собой конечное множество.
K{\ displaystyle {\ mathfrak {K}}} Ф.⊂Р.d(d целое число,d≥2){\ Displaystyle F \ подмножество \ mathbb {R} ^ {d} \; (d {\ text {integer}} \ ;, \; d \ geq 2)} Kзнак равно(Л.,г,Э.){\ Displaystyle {\ mathfrak {K}} = ({\ mathfrak {L}}, {\ mathfrak {G}}, E)}Л.{\ displaystyle {\ mathfrak {L}}}г{\ Displaystyle {\ mathfrak {G}}} Ф.{\ displaystyle F}Э.⊂Ф.{\ displaystyle E \ subset F}

Это

из в и ассоциированном наборе узлов .г{\ Displaystyle {\ mathfrak {G}}}Ф.{\ displaystyle F}Э.{\ displaystyle E}
Э.{\ displaystyle E}состоит из тех и только тех точек , из которого происходят в качестве для одной из кривых Жордана .Ф.{\ displaystyle F}г∈г{\ displaystyle g \ in {\ mathfrak {G}}}
В комплект системы состоит именно из в наборе комплемента .Л.{\ displaystyle {\ mathfrak {L}}} Ф.∖⋃г{\ Displaystyle F \ setminus \ bigcup {\ mathfrak {G}}}

Здесь каждый элемент ИС упоминается как земля , каждый элемент в качестве разграничительной линии , и каждый элемент в углу топологической карты .Л.{\ displaystyle {\ mathfrak {L}}}г{\ Displaystyle {\ mathfrak {G}}}Э.{\ displaystyle E}K{\ displaystyle {\ mathfrak {K}}}

Точка является край точка страны , принадлежащей к карте , если она принадлежит к относительному топологического замыкания в ин .Икс∈Р.d{\ Displaystyle х \ в \ mathbb {R} ^ {d}}Л.{\ displaystyle L} Л.¯∩Ф.{\ displaystyle {\ overline {L}} \ cap F}Л.{\ displaystyle L}Ф.{\ displaystyle F}

Две страны и страны называются соседними или соседними странами, если одна из них находится под линиями границ, которые полностью состоят из пограничных точек как от, так и от .Л.1{\ displaystyle L_ {1}}Л.2{\ displaystyle L_ {2}}K{\ displaystyle {\ mathfrak {K}}}K{\ displaystyle {\ mathfrak {K}}}Л.1{\ displaystyle L_ {1}}Л.2{\ displaystyle L_ {2}}

Отображение дано на целое число называется окрашиванием .
п>{\ displaystyle n> 0} жЛ.→{1,…,п}{\ Displaystyle е \ двоеточие \, {\ mathfrak {L}} \ to \ {1, \ ldots, n \}}п{\ displaystyle n}

Элементы называются

цветами (в соответствии с соглашениями теории графов ) .{1,…,п}{\ Displaystyle \ {1, \ ldots, п \}}
Окрашивание будет разрешено , если каждая две соседних стран добродетель всегда два разных цвета назначены.п{\ displaystyle n}жЛ.→{1,…,п}{\ Displaystyle е \ двоеточие \, {\ mathfrak {L}} \ to \ {1, \ ldots, n \}}ж{\ displaystyle f}

Позволяет топологическую карту на целое число в допустимых окрашивания , но не разрешается окраска менее чем цвет, мы называем это целое число от хроматического числа и обозначается .K{\ displaystyle {\ mathfrak {K}}}Ф.{\ displaystyle F}п>{\ displaystyle n> 0}п{\ displaystyle n}п{\ displaystyle n}п{\ displaystyle n}K{\ displaystyle {\ mathfrak {K}}}χ(K){\ Displaystyle \ чи ({\ mathfrak {K}})}

Если один образует более все топологические отображения наФ.{\ displaystyle F} в супремуму суп{χ(K)Kтопологическая карта на F.}{\ displaystyle \ sup \ {\ chi ({\ mathfrak {K}}): {\ mathfrak {K}} \; {\ text {топологическая карта на F}} \}} всех связанные хроматических чисел и это целое число , то это хроматические число из . Обозначается значком .<∞{\ Displaystyle <\ infty}Ф.{\ displaystyle F}χ(Ф.){\ Displaystyle \ чи (F)}

Дизайн карты

Дизайн и производство карт — это ремесло, которое развивалось на протяжении тысячелетий, от глиняных табличек до географических информационных систем . Как форма дизайна , особенно тесно связанная с графическим дизайном , создание карт включает в себя научные знания о том, как используются карты, интегрированные с принципами художественного выражения, для создания эстетически привлекательного продукта, несет ауру авторитета и функционально служит определенной цели. для целевой аудитории.

Создание карты включает объединение нескольких элементов и принятие большого количества решений. Элементы дизайна делятся на несколько широких тем, каждая из которых имеет свою собственную теорию, свою исследовательскую программу и свои собственные передовые практики. Тем не менее, между этими элементами существуют синергетические эффекты, а это означает, что общий процесс проектирования — это не просто работа над каждым элементом по отдельности, но итеративный процесс обратной связи по корректировке каждого для достижения желаемого гештальта .

Картографические проекции : основой карты является плоскость, на которой она покоится (будь то бумага или экран), но проекции необходимы, чтобы выровнять поверхность земли. Все проекции искажают эту поверхность, но картограф может стратегически определить, как и где происходит искажение.
Обобщение : все карты должны быть нарисованы в меньшем масштабе, чем реальность, что требует, чтобы информация, содержащаяся на карте, была очень маленькой выборкой из множества сведений о месте. Обобщение — это процесс настройки уровня детализации географической информации в соответствии с масштабом и назначением карты с помощью таких процедур, как выбор, упрощение и классификация.
Символика : любая карта визуально представляет местоположение и свойства географических явлений с помощью символов карты, графических изображений, состоящих из нескольких визуальных переменных , таких как размер, форма, цвет и узор.
Композиция: поскольку все символы собраны вместе, их взаимодействие оказывает большое влияние на чтение карты, такое как и визуальная иерархия .
Типографика или надписи : текст служит нескольким целям на карте, особенно помогает распознавать объекты, но надписи должны быть хорошо спроектированы и размещены, чтобы быть эффективными.
Макет : изображение карты должно быть размещено на странице (на бумаге, в Интернете или на другом носителе) вместе со связанными элементами, такими как заголовок, легенда, дополнительные карты, текст, изображения и т. Д. У каждого из этих элементов есть свои особенности дизайна, как и их интеграция, которая в значительной степени соответствует принципам графического дизайна .
Конструкция для конкретного типа карты. Различные типы карт, особенно тематические , имеют свои собственные потребности в дизайне и передовые методы.

Расстояния и масштабы

В зависимости от масштаба карты предоставляют читающим более или менее детальную информацию о местности. Соотношение линий действительным размерам местности стандартно указывается на нижней или боковой сторонах плана. Оно имеет вид дроби и показывает, во сколько раз каждая линяя чертежа меньше ее реальных размеров.

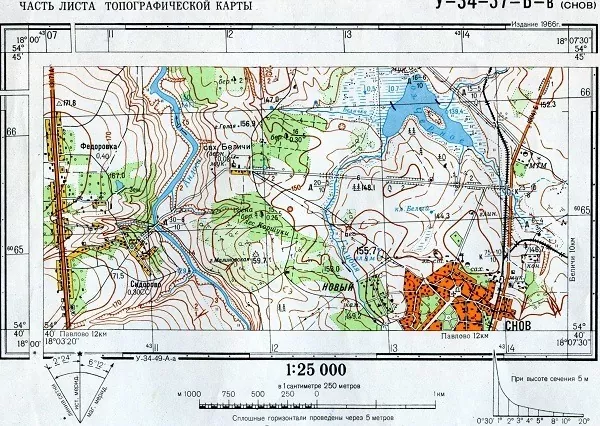
Указание масштаба на карте

Числитель всегда равен единице, а знаменатель показывает величину масштаба. Чем больше знаменатель, тем мельче масштаб карты, а значит менее детальная информация о представленной местности.

Как определить расстояние?

Чтобы определить расстояние на топографической карте между двумя объектами, нужно измерить их отдаленность обычной линейкой и умножить это число на знаменатель масштабной дроби. Результат получится в метрах.

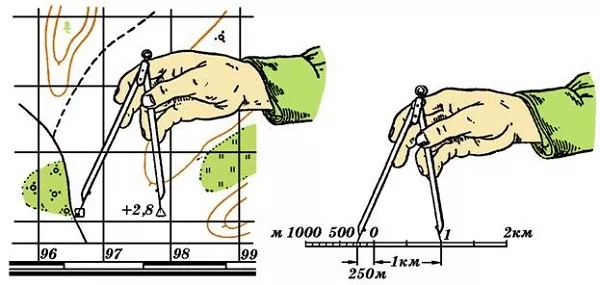
Измерение расстояния раствором циркуля

Существует еще один простой способ определения расстояния на чертеже. Он не требует никаких вычислений. Для этого нужно взять циркуль, наложить его ножки на объекты, между которыми нужно определить расстояние, а затем приложить неизмененный раствор циркуля к линейному масштабу. Количество отсчетов между ножками циркуля будет являться расстоянием между заданными точками на карте.

LО том, как читать масштаб, подробно рассказываю в статье: Как по масштабу определить расстояние на карте в походе

Использование карт с различными масштабами

Топографические карты с масштабом 1: 5000 считаются наиболее информативными. На плане с такой детализацией изображаются даже небольшие постройки, местная растительность и грунты.

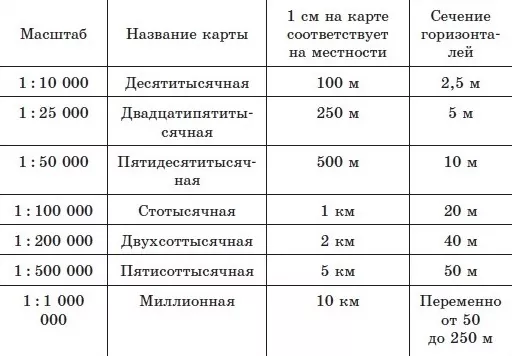
Распространенные масштабы карт

Для районов, не имеющих большого количества деревьев, оптимальным вариантом являются карты с соотношением линий 1:10000 и 1:25000. Они хорошо отображают населенные пункты, предприятия, дороги, заболоченную местность и границы. Планы с такими масштабами очень популярны для использования в хозяйственных нуждах и туристических походах.

Топографические чертежи с еще более мелким масштабом несут общее представление о местности.

Больше структуры

Часто на многообразии требуется больше структуры, чем просто топологическая структура. Например, если нужно однозначное понятие дифференцирования функций на многообразии, необходимо построить атлас, функции переходов которого дифференцируемы . Такое многообразие называется дифференцируемым . Для дифференцируемого многообразия можно однозначно определить понятие касательных векторов, а затем производных по направлениям .

Если каждая функция перехода является гладкой картой , то атлас называется гладким атласом , а само многообразие называется . В качестве альтернативы можно было бы потребовать, чтобы карты переходов имели только k непрерывных производных, и в этом случае называется атлас .
C k {\ displaystyle C ^ {k}}

Вообще говоря, если каждая функция перехода принадлежит псевдогруппе гомеоморфизмов евклидова пространства, то атлас называется -атласом. Если карты переходов между картами атласа сохраняют локальную тривиализацию , то атлас определяет структуру пучка волокон.
г {\ Displaystyle {\ mathcal {G}}} г {\ Displaystyle {\ mathcal {G}}}

Цели

Цель топографии — определить положение любого объекта или, в более общем смысле, любой точки с точки зрения как горизонтальной системы координат, такой как широта, долгота и высота . Выявление (именование) особенностей и распознавание типичных структур рельефа также являются частью поля.

Топографическое исследование может быть сделано по ряду причин: военное планирование и геолого — разведочные работы были первичные мотиваторами для начала программы обследований, но подробная информации о местности и особенности поверхности имеет важное значение для планирования и строительства любого крупного гражданского строительства , коммунальное строительство , или мелиоративные проекты.

Ориентация карт

Херефордская карта от около 1300, Херефорда собор , Англия, является классическим «TO» карта с Иерусалимом в центре, на востоке к вершине, в Европе в левом нижнем углу и в Африке справа.

Ориентация карты — это взаимосвязь между направлениями на карте и соответствующими направлениями компаса в реальности. Слово « восток » происходит от латинского oriens , что означает восток. В средние века многие карты, в том числе карты T и O , рисовались с востоком вверху (это означает, что направление «вверх» на карте соответствует Востоку на компасе). Наиболее распространенное картографическое соглашение — север находится в верхней части карты.

Карты, не ориентированные на север вверху:

Карты из незападных традиций ориентированы по-разному. На старых картах Эдо японский императорский дворец показан не только в верхней части, но и в центре карты. Ярлыки на карте ориентированы таким образом, что вы не сможете их правильно прочитать, если не поместите императорский дворец над головой.
Средневековые европейские карты T и O, такие как Hereford Mappa Mundi, были сосредоточены на Иерусалиме с Востоком вверху. Действительно, до того, как география Птолемея была повторно введена в Европу около 1400 г., на Западе не существовало единой конвенции. Карты-портоланы , например, ориентированы на описываемые ими берега.
Карты городов, граничащих с морем, часто имеют условную ориентацию с морем вверху.
Карты маршрутов и каналов традиционно ориентированы на дорогу или водный путь, которые они описывают.
Полярные карты по Арктике или Антарктике регионов обычно сосредоточены на шесте; направление на север будет соответственно к центру карты или от него. Типичные карты Арктики имеют меридиан 0 ° внизу страницы; карты Антарктики имеют меридиан 0 ° вверху страницы.
Карты в перевернутом виде, также известные как карты «вверх ногами» или « карты с ориентацией на юг» , перевернуты по соглашению « север вверху» и юг вверху. Древние африканцы, в том числе в Древнем Египте, использовали эту ориентацию, как и некоторые карты в Бразилии сегодня.
Buckminster Fuller «s Dymaxion карты основаны на проекции земной сферы на качестве икосаэдра . Полученные треугольные части могут быть расположены в любом порядке или ориентации.

Методы

Существует множество подходов к изучению топографии. Какой метод (ы) использовать, зависит от масштаба и размера исследуемой территории, ее доступности и качества существующих съемок.

Полевое исследование

Геодезический пункт в Германии

Съемка помогает точно определять положение точек в земном или трехмерном пространстве, а также расстояния и углы между ними с помощью нивелирных инструментов, таких как теодолиты , нивелиры и клинометры .

Работа над одной из первых топографических карт была начата во Франции Джованни Доменико Кассини , великим итальянским астрономом.

Несмотря на то, что дистанционное зондирование значительно ускорило процесс сбора информации и позволило повысить точность контроля на больших расстояниях, прямая съемка по-прежнему обеспечивает основные контрольные точки и основу для всех топографических работ, как вручную, так и на основе ГИС .

В областях, где проводилась обширная программа прямой съемки и картографии (например, большая часть Европы и континентальной части США), скомпилированные данные составляют основу базовых наборов цифровых данных о высотах, таких как данные USGS DEM . Эти данные часто необходимо «очищать», чтобы устранить расхождения между опросами, но они по-прежнему составляют ценный набор информации для крупномасштабного анализа.

Первоначальная американская топографическая съемка (или британская «съемка боеприпасов») включала не только запись рельефа, но и определение характерных особенностей и растительного покрова земли.

Методологии пассивных датчиков

Помимо их роли в фотограмметрии, аэрофотоснимки и спутниковые снимки могут использоваться для идентификации и обозначения особенностей местности и более общих особенностей земного покрова. Конечно, они становятся все более и более частью геовизуализации , будь то карты или системы ГИС . Отображение спектров в ложных и невидимых цветах также может помочь в определении рельефа местности путем более четкого определения растительности и другой информации о землепользовании. Изображения могут быть в видимых цветах и в другом спектре.

Фотограмметрия

Фотограмметрия — это метод измерения, при котором координаты точек в трехмерном изображении объекта определяются измерениями, выполненными на двух фотографических изображениях (или более), снятых с разных позиций, обычно из разных проходов полета с аэрофотосъемкой. В этой технике общие точки идентифицируются на каждом изображении. Линия обзора (или луч ) может быть построена от места расположения камеры до точки на объекте. Именно пересечение его лучей ( триангуляция ) определяет относительное трехмерное положение точки. Для получения абсолютных значений этих относительных положений можно использовать известные контрольные точки. Более сложные алгоритмы могут использовать другую информацию о сцене, известную априори (например, симметрии в некоторых случаях, позволяющие восстанавливать трехмерные координаты, начиная с одной единственной позиции камеры).

Активные сенсорные методики

Спутниковое радиолокационное картирование — один из основных методов создания цифровых моделей рельефа (см. Ниже). Подобные методы применяются в батиметрических съемках с использованием гидролокатора для определения рельефа дна океана. В последние годы, ЛИДАРа ( LI GHT D etection A — й R anging), метод дистанционного зондирования , который использует лазер вместо радиоволн, все чаще используют для комплексного картирования потребностей , таких как навесы графиков и мониторинга ледников.